|

전통 창호의 격자 무늬

|
|
|
|
|
|
|
|
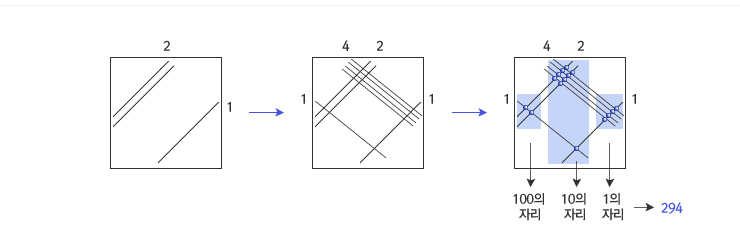
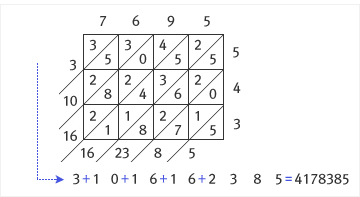
21×14를 선긋기 계산법으로 계산하는 과정

|
|
|
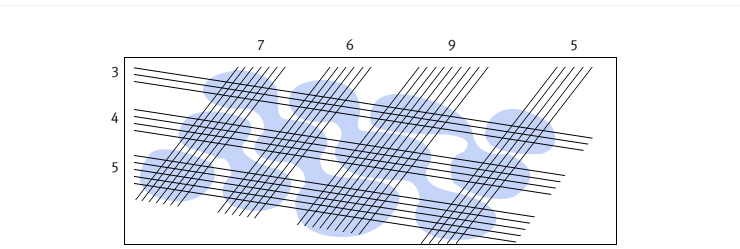
7695×543=4178385를 계산한 모습. 선긋기 계산법은 숫자가 커지면 불편해진다.

|
- 격자곱셈법(겔로시아 곱셈법)
수학에서 격자를 이용한 곱셈법. 이 방법을 ‘격자’라는 뜻의 ‘겔로시아(Gelosia)’라고 불렀다. 인도에서 최초로 개발된 것으로 추측된다.
- 선긋기 계산법
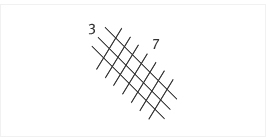
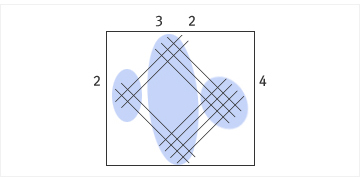
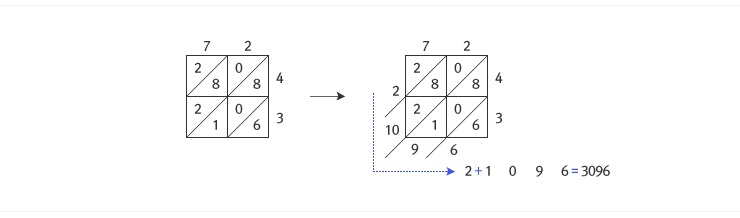
곱셈을 선을 그어서 계산하는 방법. 곱셈의 원리에 충실한 방법이다. 곱셈할 두 수를 자리수 별로 나누어 선을 교차하게 그은 후 묶어서 세는 방법으로 계산한다.

- 글 이광연 / 한서대학교 수학과 교수
- 성균관대학교 수학과를 졸업하고 와이오밍 대학교에서 박사후 과정을 밟았다. 저서로는 [웃기는 수학이지 뭐야], [수학자들의 전쟁], 2008년 문화체육관광부 우수과학도서로 선정된 [수학블로그] 등이 있다.
출처 : 네이버캐스트 :: 오늘의 과학
링크 : http://navercast.naver.com/science/math/2550
'뉴스/기사 > · 정보' 카테고리의 다른 글
| 노트북 수명을 늘리는 4가지 간단한 방법 (0) | 2010.08.19 |
|---|---|
| LG 넷하드 NT1 출시기념 무료체험 이벤트 (0) | 2010.05.31 |
| 베타 테스터 응모글 (0) | 2010.03.03 |
| Super Macro Your Cellphone Camera With A DVD Lens - 핸드폰으로 접사 (0) | 2009.08.28 |
| Möbius strip music box (0) | 2009.08.28 |